Differentiate with respect to if .

Let u = cos^–1(4x³ – 3x) and

We need to differentiate u with respect to v that is find.

We have u = cos^–1(4x³ – 3x)

By substituting x = cos θ, we have

u = cos^–1(4cos³θ – 3cosθ)

But, cos3θ = 4cos³θ – 3cosθ

⇒ u = cos^–1(cos3θ)

Given,

However, x = cos θ

Hence, u = cos^–1(cos3θ) = 3θ

⇒ u = 3cos^–1x

On differentiating u with respect to x, we get

We know

Now, we have

By substituting x = cos θ, we have

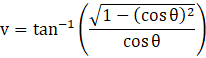
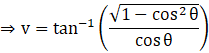
[∵ sin²θ + cos²θ = 1]

⇒ v = tan^–1(tanθ)

However,

Hence, v = tan^–1(tanθ) = θ

⇒ v = cos^–1x

On differentiating v with respect to x, we get

We know

We have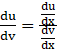

Thus,