Show that the points (3, 4), (–5, 16), (5, 1) are collinear.
Let us understand that, two more points are said to be collinear if they all lie on a single straight line.
Let the points be A (3, 4), B (–5, 16) and C (5, 1).
Let
![]()
![]()
![]()
So, in this case if we prove that ![]() and
and ![]() are parallel to each other, then we can easily show that A, B and C are collinear.
are parallel to each other, then we can easily show that A, B and C are collinear.
Therefore, ![]() is given by
is given by
![]()
![]()
![]()
![]()
![]()
And ![]() is given by
is given by
![]()
![]()
![]()
![]()
![]()
Let us note the relation between ![]() and
and ![]() .
.
We know, ![]()
Or ![]() …(i)
…(i)
And we know, ![]()
Or ![]()
Or ![]() …(ii)
…(ii)
Substituting the value of ![]() in equation (i), we get
in equation (i), we get
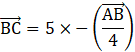
![]()
This relation shows that ![]() and
and ![]() are parallel to each other.
are parallel to each other.
But also, ![]() is the common vector in
is the common vector in ![]() and
and ![]() .
.
⇒ ![]() and
and ![]() are not parallel but lies on a straight line.
are not parallel but lies on a straight line.
Thus, A, B and C are collinear.
9