Show that the four points having position vectors are coplanar.

Question

Philoid · Accepted Answer

Vectors parallel to the same plane, or lie on the same plane are called coplanar vectors

The three vectors are coplanar if one of them is expressible as a linear combination of the other two.

Let the four points be denoted be P, Q, R and S for , , and respectively such that we can say,

Let us find , and .

So,

Also,

And,

Now, we need to show a relation between , and .

So,

Comparing coefficients of , and , we get

–6x – 4y = 10 …(i)

10x + 2y = –12 …(ii)

–6x + 10y = –4 …(iii)

For solving equation (i) and (ii) for x and y, multiply equation (ii) by 2.

10x + 2y = –12 [× 2

⇒ 20x + 4y = –24 …(iv)

Solving equations (iv) and (i), we get

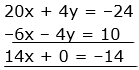
⇒ 14x = –14

⇒ x = –1

Put x = –1 in equation (i), we get

–6(–1) – 4y = 10

⇒ 6 – 4y = 10

⇒ –4y = 10 – 6

⇒ –4y = 4

⇒ y = –1

Substitute x = –1 and y = –1 in equation (iii), we get

–6x + 10y = –4

⇒ –6(–1) + 10(–1) = –4

⇒ 6 – 10 = –4

⇒ –4 = –4

∵, L.H.S = R.H.S

⇒ The value of x and y satisfy equation (iii).

Thus, , , and are coplanar.