Prove that the following vectors are coplanar :

and

We have been given that, , and .

We can form a relation using these three vectors. Say,

Comparing coefficients of , and , we get

1 = 2x – y …(1)

1 = 3x – 2y …(2)

1 = –x + 2y …(3)

Solving equations (1) and (2) for x and y.

Equation (1), 2x – y = 1

Equation (2), 3x – 2y = 1

Multiply equation (1) by 2.

2x – y = 1 [× 2

⇒ 4x – 2y = 2 …(4)

Solving equations (4) and (2), we get

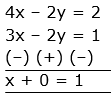
⇒ x = 1

Put x = 1 in equation (1), we get

1 = 2x – y

⇒ 1 = 2(1) – y

⇒ 1 = 2 – y

⇒ y = 2 – 1

⇒ y = 1

Substituting x = 1 and y = 1 in equation (3), we get

1 = –x + 2y

Or –x + 2y = 1

⇒ –(1) + 2(1) = 1

⇒ –1 + 2 = 1

⇒ 1 = 1

∵, L.H.S = R.H.S

⇒ The value of x and y satisfy equation (3).

Thus, , and are coplanar.