If  find
find  at
at 
We are given with an equation y = {logcosxsinx} {logsinxcosx} – 1 + sin – 1(![]() ), we have to find
), we have to find ![]() at
at
x = ![]() by using the given equation, so by differentiating the equation on both sides with respect to x, we get,
by using the given equation, so by differentiating the equation on both sides with respect to x, we get,
By using the properties of logarithms,
y = {logcosxsinx}2 + sin – 1(![]() )
)
y = {![]() }2 + sin – 1(
}2 + sin – 1(![]() )
)
![]() = 2{
= 2{![]() }
} 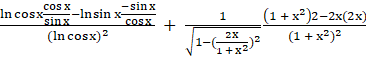
![]() = 2{
= 2{![]() }
} ![]()
![]() = 2{
= 2{![]() }
} ![]()
Now putting the value of x = ![]() in the derivative solved above, we get,
in the derivative solved above, we get,
![]() (x = π/4) = 2{1}
(x = π/4) = 2{1}  +
+ ![]()
![]() (x = π/4) = 2{1}
(x = π/4) = 2{1} 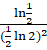 +
+ ![]()
![]() (x = π/4) = 2{1}
(x = π/4) = 2{1} ![]() +
+ ![]()
![]() (x = π/4) =
(x = π/4) = ![]() +
+ ![]()
30