If the lines 
and 
are perpendicular, find the value of k and hence find the equation of the plane containing these lines.
The direction ratio of the line 
is r1 = (– 3, – 2k, 2)
The direction ratio of the line 
is r2 = (k, 1, 5)
Since the line 
and 
are perpendicular so
r1.r2 = 0
(– 3, – 2k, 2). (k, 1, 5) = 0
– 3k – 2k + 10 = 0
– 5k = – 10
k = 2
the equation of the line are 
and 
The equation of the plane containing the perpendicular lines 
and 
is
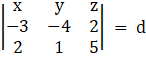
(– 20 – 2)x – y(– 15 – 4) + z(– 3 + 8) = d
– 22x + 19y + 5z = d
The line 
pass through the point (1, 2, 3) so putting x = 1, y = 2, z = 3 in the equation – 22x + 19y + 5z = d we get
– 22(1) + 19(2) + 5(3) = d
d = – 22 + 38 + 15
d = 31
The equation of the plane containing the lines is – 22x + 19y + 5z = 31
9