Show that the lines 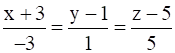 and
and 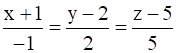 are coplanar. Hence, find the equation of the plane containing these lines.
are coplanar. Hence, find the equation of the plane containing these lines.
We know that the lines ![]() are coplanar if
are coplanar if
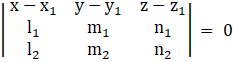
Here,
x1 = –3, x1 = –1, y1 = 1, y2 = 2, z1 = 5, z2 = 5
l1 = –3, l2 = –1, m1 = 1, m2 = 2, n1 = 5, n2 = 5
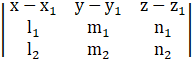
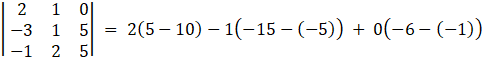
= 2(–5) – 1(–10) = – 10 + 10
= 0
So the given line are coplanar .
The equation of plane contains lines is 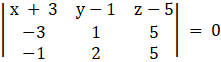
(x + 3)(5 – 10) – (y – 1)(– 15 – (– 5)) + (z – 5)(– 6 – (– 1)) = 0
– 5x – 15 + 10y – 10 – 5z + 25 = 0
– 5x + 10y – 5z = 0
Divided by – 5
x – 2y + z = 0
14