If y = 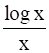, show that .

Question

Philoid · Accepted Answer

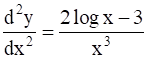Basic idea:

√Second order derivative is nothing but derivative of derivative i.e.

√The idea of chain rule of differentiation: If f is any real-valued function which is the composition of two functions u and v, i.e. f = v(u(x)). For the sake of simplicity just assume t = u(x)

Then f = v(t). By chain rule, we can write the derivative of f w.r.t to x as:

√Product rule of differentiation-

√Apart from these remember the derivatives of some important functions like exponential, logarithmic, trigonometric etc..

Let’s solve now:

Given, y = …..equation 1

As we have to prove : ..

We notice a second-order derivative in the expression to be proved so first take the step to find the second order derivative.

Let’s find

As

So, lets first find dy/dx and differentiate it again.

As y is the product of two functions u and v

Let u = log x and v = 1/x

Using product rule of differentiation:

[∵ log x) = & ]

Again using the product rule to find :

[∵ log x) = & ]

∴ ….. proved