The radius of a cylinder is increasing at the rate 2 cm/sec and its altitude is decreasing at the rate of 3 cm/sec. Find the rate of change of volume when radius is 3 cm and altitude 5cm.

Question

Philoid · Accepted Answer

Given: the radius of a cylinder is increasing at the rate 2 cm/sec and its altitude is decreasing at the rate of 3 cm/sec

To find the rate of change of volume when radius is 3 cm and altitude 5cm

Let V be the volume of the cylinder, r be its radius and h be its altitude at any instant of time ‘t’.

We know volume of the cylinder is

V = r²h

Differentiating this with respect to time we get

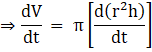
Now will apply the product rule of differentiation, i.e.,

, so the above equation becomes,

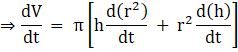
But given of a cylinder is increasing at the rate 2 cm/sec, i.e., and its altitude is decreasing at the rate of 3 cm/sec, i.e., , by subsitituting the above values in equation (i) we get

When radius of the cylinder, r = 3cm and its altitude, h = 5cm, the equation (ii) becomes,

Hence the rate of change of volume when radius is 3 cm and altitude 5cm is 33 cm³/sec