The volume of metal in a hollow sphere is constant. If the inner radius is increasing at the rate of 1 cm/sec, find the rate of increase of the outer radius when the radii are 4 cm and 8cm respectively.

Question

Philoid · Accepted Answer

Let the inner radius be r, outer radius be R and volume be V of a hollow sphere at any instant of time

We know the volume of the hollow sphere is

Differentiating the volume with respect to time, we get

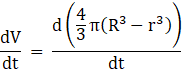
This is the rate of the volume of the hollow sphere and it is given this is constant hence

Given that the rate of increase in inner radius of the hollow sphere,, So the above equation becomes,

So when the radii are 4cm and 8 cm, the above equation becomes,

Therefore the rate of increase of the outer radius when the radii are 4 cm and 8cm respectively is 0.25 cm/sec