The volume of a spherical balloon is increasing at the rate of 25 cm³/sec. Find the rate of change of its surface area at the instant when the radius is 5 cm.

Given: the volume of a spherical balloon is increasing at the rate of 25 cm³/sec.

To find the rate of change of its surface area at the instant when the radius is 5 cm

Let the radius of the given spherical balloon be r cm, and V be its volume at any instant time.

Then according to the given criteria,

The rate of the volume of the spherical balloon is increasing is,

But volume of the spherical balloon is,

Applying derivative with respect to time on both sides we get,

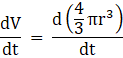
Substituting the value from equation (i) in above equation, we get

Now the surface area of the spherical balloon at any time t will be

S = 4r² cm².

Applying derivative with respect to time on both sides we get,

Substituting the value from equation (ii), we get

So when the radius is 5cm, the rate of surface area will become,

Hence the rate of change of its surface area at the instant when the radius is 5 cm is 10cm²/sec