For the binary operation x7 on the set of S = {1, 2, 3, 4, 5, 6} compute 3 – 1x74.
A composition table consists of elements which are a result of an operation on the set elements.
Here we have the operation, a x7b = remainder of ab divided by 7 where a, b ![]() S.
S.
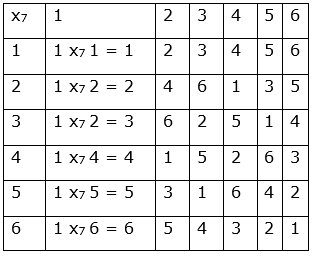
For b![]() S to be an inverse of a
S to be an inverse of a![]() S, a x7b = e, where e is the identity element.
S, a x7b = e, where e is the identity element.
We know for multiplication operation we have the identity element as 1.
So e = 1.
For a = 3,
3 x7 (inverse of 3) = 1
![]()
From the table above, 3 x7 5 = 1
Hence we can conclude that ‘inverse of 3’ must be 5.
Therefore the expression:
3 – 1 x7 4 = 5 x7 4 = 6. (From the table above)
6