Show that 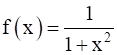 decreases in the interval [0, ∞) and increases in the interval (-∞, 0].
decreases in the interval [0, ∞) and increases in the interval (-∞, 0].
We have,
![]()
Case 1
When x![]() [0,
[0,![]() )
)
Let ![]() ,
, ![]() (0,
(0,![]() ] and
] and ![]()
⇒ ![]()
⇒ ![]()
⇒ ![]()
⇒ f(x1)< f(x2)
![]() f(x) is decreasing on[0,∞).
f(x) is decreasing on[0,∞).
Case 2
When x![]() (-
(-![]() ,0]
,0]
Let ![]() >
> ![]()
⇒ ![]()
⇒ ![]()
⇒ ![]()
⇒ ![]()
![]() f(x) is increasing on(-∞,0].
f(x) is increasing on(-∞,0].
Thus, f(x) is neither increasing nor decreasing on R.
6