Solve the following system of the linear equations by Cramer’s rule:

x + y + z + 1 = 0

ax + by + cz + d = 0

a²x + b²y + c²z + d² = 0

Given: - Equations are: –

x + y + z + 1 = 0

ax + by + cz + d = 0

a²x + b²y + c²z + d² = 0

Tip: - Theorem – Cramer’s Rule

Let there be a system of n simultaneous linear equations and with n unknown given by

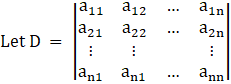
and let D_j be the determinant obtained from D after replacing the j^th column by

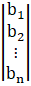
Then,

provided that D ≠ 0

Now, here we have

x + y + z + 1 = 0

ax + by + cz + d = 0

a²x + b²y + c²z + d² = 0

So by comparing with theorem, lets find D , D₁ , D₂ and D₃

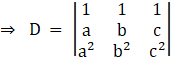
applying,

⇒

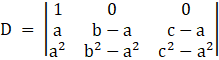
Take (b – a) from c₂ , and (c – a) from c₃ common, we get

⇒

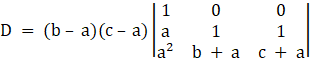
Solving determinant, expanding along 1^st Row

⇒ D = (b – a)(c – a)1[c + a – (b + a)]

⇒ D = (b – a)(c – a)(c + a – b – a)

⇒ D = (b – a)(c – a)(c – b)

⇒ D = (a – b)(b – c)(c – a)

Again, Solve D₁ formed by replacing 1^st column by B matrices

Here

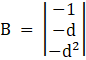
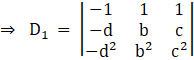
applying,

⇒

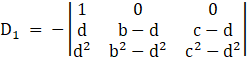
Take (b – d) from c₂ , and (c – d) from c₃ common, we get

⇒

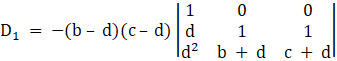
Solving determinant, expanding along 1^st Row

⇒ D₁ = – (b – d)(c – d)1[c + d – (b + d)]

⇒ D₁ = – (b – d)(c – d)(c + d – b – d)

⇒ D₁ = – (b – d)(c – d)(c – b)

⇒ D₁ = – (d – b)(b – c)(c – d)

Again, Solve D₂ formed by replacing 2^nd column by B matrices

Here

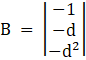
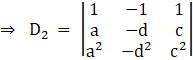
applying,

⇒

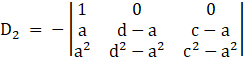
Take (d – a) from c₂ , and (c – a) from c₃ common, we get

⇒

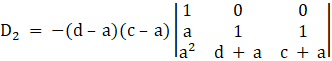
Solving determinant, expanding along 1^st Row

⇒ D₂ = – (d – a)(c – a)1[c + a – (d + a)]

⇒ D₂ = – (d – a)(c – a)(c + a – d – a)

⇒ D₂ = – (d – a)(c – a)(c – d)

⇒ D₂ = – (a – d)(d – c)(c – a)

And, Solve D₃ formed by replacing 3^rd column by B matrices

Here

⇒

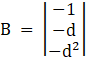
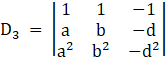
applying,

⇒

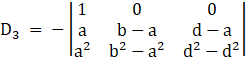
Take (b – a) from c₂ , and (d – a) from c₃ common, we get

⇒

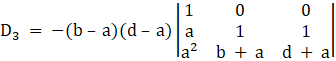
Solving determinant, expanding along 1^st Row

⇒ D₃ = – (b – d)(c – d)1[a + d – (b + a)]

⇒ D₃ = – (b – d)(c – d)(a + d – b – a)

⇒ D₃ = – (b – d)(c – d)(d – b)

⇒ D₃ = – (d – b)(b – d)(c – d)

Thus by Cramer’s Rule, we have

⇒

⇒

again,

⇒

⇒

and,

⇒

⇒