Show that each of the following systems of linear equations is inconsistent:

3x – y + 2z = 3

2x + y + 3z = 5

x – 2y – z = 1

Given: - Three equation

3x – y + 2z = 3

2x + y + 3z = 5

x – 2y – z = 1

Tip: - We know that

For a system of 3 simultaneous linear equation with 3 unknowns

(i) If D ≠ 0, then the given system of equations is consistent and has a unique solution given by

(ii) If D = 0 and D₁ = D₂ = D₃ = 0, then the given system of equation may or may not be consistent. However if consistent, then it has infinitely many solutions.

(iii) If D = 0 and at least one of the determinants D₁, D₂ and D₃ is non – zero, then the system is inconsistent.

Now,

We have,

3x – y + 2z = 3

2x + y + 3z = 5

x – 2y – z = 1

Lets find D

⇒

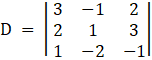
Expanding along 1^st row

⇒ D = 3[ – 1 – 3( – 2)] – ( – 1)[( – 1)2 – 3] + 2[ – 4 – 1]

⇒ D = 3[5] + 1[ – 5] + 2[ – 5]

⇒ D = 0

Again, D₁ by replacing 1^st column by B

Here

⇒

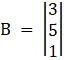
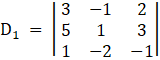
⇒ D₁ = 3[ – 1 – 3( – 2)] – ( – 1)[( – 1)5 – 3] + 2[ – 10 – 1]

⇒ D_{1 =} 3[5] + [ – 8] + 2[ – 11]

⇒ D_{1 =} 15 – 8 – 22

⇒ D₁ = – 15

⇒ D₁ ≠ 0

So, here we can see that

D = 0 and D₁ is non – zero

Hence the given system of equation is inconsistent.

Hence Proved