Show that each of the following systems of linear equations has infinite number of solutions and solve:

x – y + 3z = 6

x + 3y – 3z = – 4

5x + 3y + 3z = 10

Given: - Three equation

x – y + 3z = 6

x + 3y – 3z = – 4

5x + 3y + 3z = 10

Tip: - We know that

For a system of 3 simultaneous linear equation with 3 unknowns

(iv) If D ≠ 0, then the given system of equations is consistent and has a unique solution given by

(v) If D = 0 and D₁ = D₂ = D₃ = 0, then the given system of equation may or may not be consistent. However if consistent, then it has infinitely many solution.

(vi) If D = 0 and at least one of the determinants D₁, D₂ and D₃ is non – zero, then the system is inconsistent.

Now,

We have,

x – y + 3z = 6

x + 3y – 3z = – 4

5x + 3y + 3z = 10

Lets find D

⇒

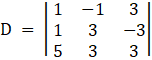
Expanding along 1^st row

⇒ D = 1[9 – ( – 3)(3)] – ( – 1)[(3)1 – 5( – 3)] + 3[3 – 5(3)]

⇒ D = 1[18] + 1[18] + 3[12]

⇒ D = 0

Again, D₁ by replacing 1^st column by B

Here

⇒

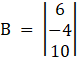
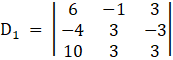
⇒ D₁ = 6[9 – ( – 3)(3)] – ( – 1)[( – 4)3 – 10( – 3)] + 3[ – 12 – 30]

⇒ D_{1 =} 6[9 + 9] + [ – 12 + 30] + 3[ – 42]

⇒ D_{1 =} 6[18] + 18 – 3[42]

⇒ D₁ = 0

Also, D₂ by replacing 2^nd column by B

Here

⇒

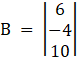
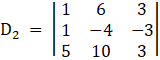
⇒ D₂ = 1[ – 12 – ( – 3)10] – 6[3 – 5( – 3)] + 3[10 – 5( – 4)]

⇒ D_{2 =} [ – 12 + 30] – 6[3 + 15] + 3[10 + 20]

⇒ D_{2 =} 18 – 6[18] + 3[30]

⇒ D₂ = 0

Again, D₃ by replacing 3^rd column by B

Here

⇒

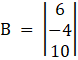
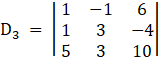
⇒ D₃ = 1[30 – ( – 4)(3)] – ( – 1)[(10 – 5( – 4)] + 6[3 – 15]

⇒ D_{3 =} 1[30 + 12] + 1[10 + 20] + 6[ – 12]

⇒ D_{3 =} 42 + 30 – 72

⇒ D₃ = 0

So, here we can see that

D = D₁ = D₂ = D₃ = 0

Thus,

Either the system is consistent with infinitely many solutions or it is inconsistent.

Now, by 1^st two equations, written as

x – y = 6 – 3z

x + 3y = – 4 + 3z

Now by applying Cramer’s rule to solve them,

New D and D₁, D₂

⇒

⇒ D = 3 + 1

⇒ D = 4

Again, D₁ by replacing 1^st column with

⇒

⇒ D₁ = 18 – 9z – ( – 1)( – 4 + 3z)

⇒ D₁ = 14 – 5z

Again, D₂ by replacing 2^nd column with

⇒

⇒ D₂ = – 4 + 3z – (6 – 3z)

⇒ D₂ = – 10 + 6z

Hence, using Cramer’s rule

⇒

⇒

⇒

again,

⇒

⇒

⇒

Let, z = k

Then

And z = k

By changing value of k you may get infinite solutions