A salesman has the following record of sales during three months for three items A,B and C which have different rates of commission.

Find out the rates of commission on items A,B and C by using determinant method.

Given: - Record of sales during three months

Let, rates of commissions on items A,B and C be x, y and z respectively.

Now, we can arrange this model in linear equation system

Thus, we have

90x + 100y + 20z = 800

130x + 50y + 40z = 900

60x + 100y + 30z = 850

Here

⇒

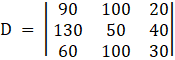
Applying,

⇒

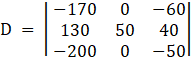
Solving determinant, expanding along 2^nd column

⇒ D = 50[( – 50)( – 170) – ( – 200)( – 60)]

⇒ D = 50[8500 – 12000]

⇒ D = – 175000

Again, Solve D₁ formed by replacing 1^st column by B matrices

Here

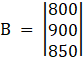
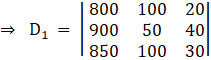
Applying,

⇒

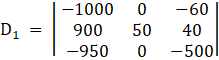
Solving determinant, expanding along 2^nd column

⇒ D₁ = 50[( – 1000)( – 500) – ( – 950)( – 60)]

⇒ D₁ = 50[50000 – 57000]

⇒ D₁ = – 350000

Again, Solve D₂ formed by replacing 2^nd column by B matrices

Here

Applying,

⇒

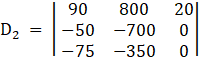
Solving determinant, expanding along 1^st Row

⇒ D₂ = 20[17500 – 52500]

⇒ D₂ = – 700000

And, Solve D₃ formed by replacing 3^rd column by B matrices

Here

⇒

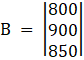
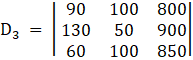
Applying,

⇒

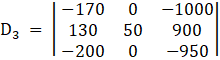
Solving determinant, expanding along 1^st Row

⇒ D₃ = 50[161500 – 200000]

⇒ D₃ = – 1925000

Thus by Cramer’s Rule, we have

⇒

⇒

⇒ x = 2

again,

⇒

⇒

⇒ y = 4

and,

⇒

⇒

z = 11

Thus rates of commission of items A, B and C are 2%, 4% and 11% respectively.