An automobile company uses three types of steel S₁, S₂ and S₃ for producing three types of cars C₁, C₂ and C₃. Steel requirements (in tons) for each type of cars are given below:

Using Cramer’s rule, find the number of cars of each type which can be produced using 29, 13 and 16 tonnes of steel of three types respectively.

Given: - Steel requirement for each car is given

Let, Number of cars produced by steel type C₁, C₂ and C₃ be x, y and z respectively.

Now, we can arrange this model in linear equation system

Thus, we have

2x + 3y + 4z = 29

x + y + 2z = 13

3x + 2y + z = 16

Here

⇒

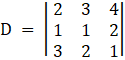
Applying,

⇒

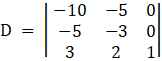
Solving determinant, expanding along 3^rd column

⇒ D = 1[30 – 25]

⇒ D = 5

⇒ D = 5

Again, Solve D₁ formed by replacing 1^st column by B matrices

Here

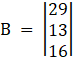
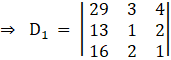
Applying,

⇒

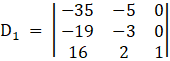
Solving determinant, expanding along 3^rd column

⇒ D₁ = 1[( – 35)( – 3) – ( – 5)( – 19)]

⇒ D₁ = 1[105 – 95]

⇒ D₁ = 10

Again, Solve D₂ formed by replacing 2^nd column by B matrices

Here

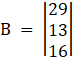
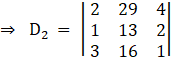
Applying,

⇒

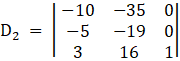
Solving determinant, expanding along 3^rd column

⇒ D₂ = 1[190 – 175]

⇒ D₂ = 15

And, Solve D₃ formed by replacing 3^rd column by B matrices

Here

⇒

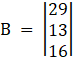
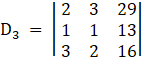
Applying,

⇒

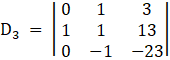
Solving determinant, expanding along 1^st column

⇒ D₃ = – 1[ – 23 – ( – 1)3]

⇒ D₃ = 20

Thus by Cramer’s Rule, we have

⇒

⇒

⇒ x = 2

again,

⇒

⇒

⇒ y = 3

and,

⇒

⇒

⇒ z = 4

Thus Number of cars produced by type C₁, C₂ and C₃ are 2, 3 and 4 respectively.