Let C be a curve defined parametrically as x = a cos3 θ, y = a sin3 θ, 0 ≤θ ≤ π/2. Determine a point P on C, where the tangent to C is parallel to the chord joining the points (a, 0) and (0, a).
sin x and cos x functions are continuous everywhere on (−∞, ∞) and differentiable for all arguments.
So both the necessary conditions of Lagrange’s mean value theorem is satisfied.
x = a cos3 θ
![]()
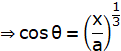
y = a sin3 θ
![]()

We know that,
sin2 θ + cos2 θ = 1

![]()
![]()

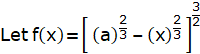
![]()
![]()
![]()
x = acos3 θ
![]()
![]()
![]()
y = asin3 θ
![]()
![]()
![]()
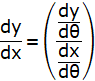
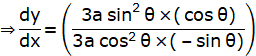
![]()
For f’(c), put the value of x=c in f’(x):
f’(c) = – tan θ
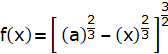
For f(a), put the value of x=a in f(x):

= 0
For f(0), put the value of x=0 in f(x):
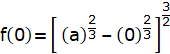

= a
![]()
![]()
![]()
⇒ – tan θ = – 1
⇒ tan θ = 1
![]()
Now put the value of θ in the function of x and y:
x = a cos3 θ
![]()

![]()
Similarly,
y = a sin3 θ
![]()
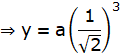
![]()
![]()
10