Find the The Slopes of the tangent and the normal to the following curves at the indicated points :
x = a cos3 θ, y = a sin3 θ at θ = π/4
Given:
x = acos3![]() & y = asin3
& y = asin3![]() at
at ![]()
Here, To find ![]() , we have to find
, we have to find ![]() &
& ![]() and and divide
and and divide 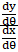 and we get our desired
and we get our desired ![]() .
.
![]() (xn) = n.xn – 1
(xn) = n.xn – 1
⇒ x = acos3![]()
⇒ ![]() = a(
= a(![]() (cos3
(cos3![]() ))
))
![]() (cosx) = – sinx
(cosx) = – sinx
⇒ ![]() = a(3cos3 – 1
= a(3cos3 – 1![]() – sin
– sin![]() )
)
⇒ ![]() = a(3cos2
= a(3cos2![]() – sin
– sin![]() )
)
⇒ ![]() = – 3acos2
= – 3acos2![]() sin
sin![]() ...(1)
...(1)
⇒ y = asin3![]()
⇒ ![]() = a(
= a(![]() (sin3
(sin3![]() ))
))
![]() (sinx) = cosx
(sinx) = cosx
⇒ ![]() = a(3sin3 – 1
= a(3sin3 – 1![]() cos
cos![]() )
)
⇒ ![]() = a(3sin2
= a(3sin2![]() cos
cos![]() )
)
⇒ ![]() = 3asin2
= 3asin2![]() cos
cos![]() ...(2)
...(2)
⇒ 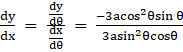
⇒ ![]()
⇒ ![]() = – tan
= – tan![]()
The Slope of the tangent is – tan![]()
Since, ![]()
⇒ ![]() = – tan(
= – tan(![]() )
)
⇒ ![]() = – 1
= – 1
![]() tan(
tan(![]() ) = 1
) = 1
![]() The Slope of the tangent at x =
The Slope of the tangent at x = ![]() is – 1
is – 1
⇒ The Slope of the normal = ![]()
⇒ The Slope of the normal = 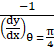
⇒ The Slope of the normal = ![]()
⇒ The Slope of the normal = 1
1