Find a point on the curve y = 3x 2 + 4 at which the tangent is perpendicular to the line whose slope is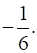

Question

Philoid · Accepted Answer

Given:

The curve y = 3x² + 4 and the Slope of the tangent is

y = 3x² + 4

Differentiating the above w.r.t x

⇒ = 23x^{2 – 1} + 0

⇒ = 6x ...(1)

Since, tangent is perpendicular to the line,

The Slope of the normal =

i.e, =

⇒ =

⇒ x = 1

Substituting x = 1 in y = 3x² + 4,

⇒ y = 3(1)² + 4

⇒ y = 3 + 4

⇒ y = 7

Thus, the required point is (1,7).

Find a point on the curve y = 3x2 + 4 at which the tangent is perpendicular to the line whose slope is