Find the point on the curve 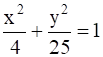 at which the tangents are parallel to the
at which the tangents are parallel to the
x – axis
Given:
The curve is ![]() = 1
= 1
Differentiating the above w.r.t x, we get the The Slope of a tangent,
⇒ ![]() = 0
= 0
Cross multiplying we get,
⇒ ![]() = 0
= 0
⇒ 50x + 8y![]() = 0
= 0
⇒ 8y![]() = – 50x
= – 50x
⇒ ![]() =
= ![]()
⇒ ![]() =
= ![]() ...(1)
...(1)
(i)
Since, the tangent is parallel to x – axis
⇒ ![]() = tan(0) = 0 ...(2)
= tan(0) = 0 ...(2)
![]() tan(0) = 0
tan(0) = 0
![]() = The Slope of the tangent = tan
= The Slope of the tangent = tan![]()
From (1) & (2),we get,
⇒ ![]() = 0
= 0
⇒ – 25x = 0
⇒ x = 0
Substituting x = 0 in ![]() = 1,
= 1,
![]() = 1
= 1
⇒ y2 = 25
⇒ y = ±5
Thus, the required point is (0,5) & (0, – 5)
17