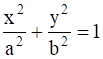Given:
Curves ![]() +
+ ![]() 1 ...(1)
1 ...(1)
& x2 + y2 = ab ...(2)
Second curve is x2 + y2 = ab
y2 = ab – x2
Substituting this in equation (1),
![]() +
+ ![]() 1
1
![]() 1
1
![]() x2b2 + a3b – a2x2 = a2b2
x2b2 + a3b – a2x2 = a2b2
![]() x2b2 – a2x2 = a2b2 – a3b
x2b2 – a2x2 = a2b2 – a3b
![]() x2(b2 – a2) = a2b(b – a)
x2(b2 – a2) = a2b(b – a)
![]() x2
x2![]()
![]() x2
x2![]()
![]() x2
x2![]()
∴a2 – b2 = (a + b)(a – b)
![]() x
x![]() ...(3)
...(3)
since , y2 = ab – x2
![]() y2 = ab – (
y2 = ab – (![]() )
)
![]() y2
y2![]()
![]() y2
y2![]()
![]() y = ±
y = ±![]() ...(4)
...(4)
since ,curves are ![]() +
+ ![]() 1 & x2 + y2 = ab
1 & x2 + y2 = ab
Differentiating above w.r.t x,
⇒ ![]() .
.![]() = 0
= 0
⇒ ![]() .
.![]() =
= ![]()
⇒ ![]()
⇒ ![]()
⇒ m1![]() ...(5)
...(5)
Second curve is x2 + y2 = ab
⇒ 2x + 2y.![]() 0
0
⇒ m2![]() ...(6)
...(6)
Substituting (3) in (4), above values for m1 & m2,we get,
At (![]() ,
, ![]() ) in equation(5),we get
) in equation(5),we get

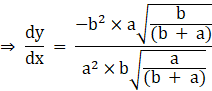
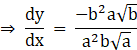
⇒ m1![]()
At (![]() ,
, ![]() ) in equation(6),we get
) in equation(6),we get
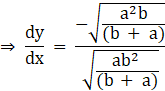
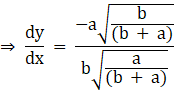
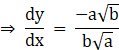
![]() m2
m2![]()
when m1![]() & m2
& m2![]()

![]() tanθ
tanθ
![]() tanθ
tanθ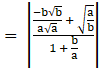
![]() tanθ
tanθ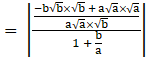
![]() tanθ
tanθ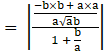
![]() tanθ
tanθ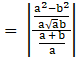
![]() tanθ
tanθ
![]() tanθ
tanθ![]()
![]() θ = tan – 1(
θ = tan – 1(![]() )
)
1