Using integration, find the area of the region bounded by the following curves, after making a rough sketch: y = 1 + |x + 1|, x = - 2, x = 3, y = 0.

Given equations are:

y = 1 + |x + 1|

y = 1 + x + 1, if x + 1 ≥ 0

y₂ = 2 + x …… (1), if x ≥ - 1

And y = 1 – (x + 1), if x + 1 < 0

y = 1 – x – 2, if x < - 1

y₁ = - x …… (2), if x < - 1

x = - 2 ...... (3)

x = 3 ...... (4)

y = 0 ...... (5)

So, equation (1) is straight line that passes thorough (0,2) and ( - 1,1). Equation (2) is a line passing through ( - 1,1) and ( - 2,2) and it is enclosed by line x = - 2 and x = 3 which are lines parallel to y – axis and pass through ( - 2,0) and (3,0) respectively, y = 0 is x – axis. So, a rough sketch of the curves is gives as: -

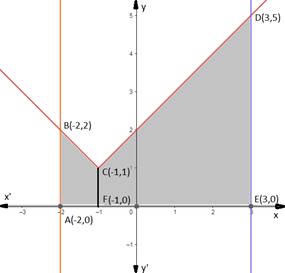
We have to find the area of shaded region.

Required area

= (shaded region ABCDEA)

= shaded region ABCFA + Shaded region FCDEFC

(the area can be found by taking a small slice in each region of width Δx, then the area of that sliced part will be yΔx as it is a rectangle and then integrating it to get the area of the whole region)

(As x is between ( - 2, - 1) in first shaded region and x is between ( - 1,3) for the second shaded region)

(from equation (1) and (2))

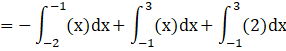
Now integrating by applying power rule, we get

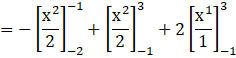
Now applying the limits we get

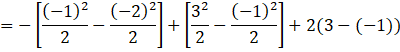
Hence the area of the region bounded by the curves, y = 1 + |x + 1|, x = - 2, x = 3, y = 0 is equal to square units.