Sketch the graph y = |x + 1|. Evaluate . What does the value of this integral represent on the graph?

Given equations are:

y = |x + 1|

y₁ = x + 1, if x + 1 ≥ 0

y₁ = x + 1 …… (1), if x ≥ - 1

And y₂ = - (x + 1), if x + 1 < 0

y₂ = - (x + 1) …… (2), if x < - 1

So, equation (1) is straight line that passes thorough ( - 1,0) and (0,1). Equation (2) is a line passing through ( - 1,0). So, the graph of which is as follows:

(As x is between ( - 4, - 1) in first shaded region equation becomes as y₂ and when x is between ( - 1,2) for the second shaded region equation becomes y₁)

(from equation (2))

Now integrating by applying power rule, we get

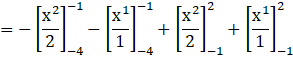
Now applying the limits we get

Hence the value of represents the area of the shaded region (as shown in the graph) and is equal to 9 square units.