Find the equation of the plane which bisects the line segment joining the points (-1, 2, 3) and (3, -5, 6) at right angles.

Question

Philoid · Accepted Answer

The given plane bisects the line segment joining points A(-1, 2, 3) and B(3, -5, 6) and is at a right angle to it.

This means the plane passes through the midpoint of the line AB

Therefore,

And it is also given the plane is normal to the line joining the points A(-1, 2, 3) and B(3, -5, 6)

Then

Position vector of - position vector of

We know that the vector equation of a plane passing through the point and perpendicular/normal to the vector is given by

Substituting the values from eqn(i) and eqn(ii) in the above equation, we get

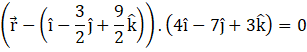
(by multiplying the two vectors using the formula )

is the vector equation of a required plane.

Let

Then, the above vector equation of the plane becomes,

Now multiplying the two vectors using the formula, we get

This is the Cartesian form of equation of the required plane.