Find the equation of the plane mid–parallel to the planes 2x – 2y + z + 3 = 0 and 2x – 2y + z + 9 = 0.

Given:

* Equation of planes: π₁= 2x – 2y + z + 3 = 0
π₂= 2x – 2y + z + 9 = 0

Let the equation of the plane mid–parallel to these planes be:

π₃: 2x – 2y + z + θ = 0

Now,

Let P(x₁,y₁,z₁) be any point on this plane,

⟹ 2(x₁) – 2(y₁) + (z₁) + θ = 0 eq(i)

We know, the distance of point (x₁,y₁,z₁) from the plane

is given by:

⟹ Distance of P from π₁:

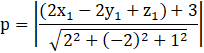
⟹ (using eq(i) )

Similarly

⟹ Distance of P from π₂ :

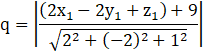
⟹ (using eq(i) )

As π₃ is mid–parallel to π₁ and π_{2 :}

p = q

⟹

Squaring both sides,

⟹

⟹ (3 – θ)² = (9 – θ)²

⟹ 9 – 6θ + θ² = 81 – 18θ + θ²

⟹ θ = 6

∴ equation of the mid–parallel plane is 2x – 2y + z + 6 = 0