In roulette, Fig. 32.2, the wheel has 13 numbers 0,1,2,….,12 marked on equally spaced slots. A player sets ₹10 on a given number. He receives ₹100 from the organizer of the game if the ball comes to rest in this slot; otherwise he gets nothing. If X denotes the player’s net gain/loss, find E (X).

As player sets Rs 10 on a number ,if he wins he get Rs 100

∴ his profit is Rs 90.

If he loses, he suffers a loss of Rs 10

He gets a profit when ball comes to rest in his selected slot.

Total possible outcome = 13

Favourable outcomes = 1

∴ probability of getting profit = 1/13

And probability of loss = 12/13

If X is the random variable denoting gain and loss of player

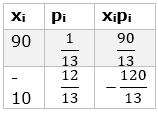
∴ X can take values 90 and -10

P(X=90) = 1/13

And P(X=-10) = 12/13

Now we have p_i and x_i.

Let’s proceed to find mean

Mean of any probability distribution is given by Mean = ∑x_ip_i

∴ first we need to find the products i.e. p_ix_i and add them to get mean

Following table representing probability distribution gives the required products :

E(X) = Mean =