If a young man drives his scooter at a speed of 25 km/hr, he has to spend Rs2 per km on petrol. If he drives the scooter at a speed of 40 km/hour, it produces air pollution and increases his expenditure on petrol to Rs 5 per km. He has a maximum of Rs100 to spend on petrol and travel a maximum distance in one hour time with less pollution. Express this problem as an LPP and solve it graphically. What value do you find here?
Let young man drives x km at a speed of 25 km/hr and y km at a speed of 40 km/hr. Clearly,
x, y ![]() 0
0
It is given that, he spends Rs 2 per km if he drives at a speed of 25 km/hr and Rs 5 per km if he drives at a speed of 40 km/hr. Therefore, money spent by him when he travelled x km and y km are Rs 2x and Rs 5y respectively.
It is given that he has a maximum of Rs 100 to spend.
Thus, 2x + 5y ![]() 100
100
Time spent by him when travelling with a speed of 25 km/hr = ![]() hr
hr
Time spent by him when travelling with a speed of 40km/hr = ![]() hr
hr
Also, the available time is 1 hour.
![]()
Or, 40x + 25y![]() 1000
1000
The distance covered is Z = x + y which is to be maximized.
Thus, the mathematical formulation of the given linear programming problem is Max Z = x + y subject to
2x + 5y ![]() 100
100
40x + 25y![]() 1000
1000
x, y ![]() 0
0
First we will convert inequations as follows:
2x + 5y = 100
40x + 25y = 1000
x = 0 and y = 0.
The region represented by 2x + 5y ![]() 100
100
The line 2x + 5y = 100 meets the coordinate axes at A(50,0) and B(0,20) respectively. By joining these points, we obtain the line 2x + 5y = 100. Clearly (0, 0) satisfies the 2x + 5y = 100. So, the region which contains the origin represents the solution set of the inequation 2x + 5y ![]() 100
100
The region represented by 40x + 25y ![]() 1000
1000
The line 40x + 25y = 1000 meets the coordinate axes at C(25,0) and D(0,40) respectively. By joining these points, we obtain the line 2x + y = 12. Clearly (0, 0) satisfies the 40x + 25y = 1000. So, the region which contains the origin represents the solution set of the inequation 40x + 25y ![]() 1000
1000
The region represented by x ![]() 0, y
0, y ![]() 0 :
0 :
Since every point in the first quadrant satisfies these inequations. So, the first quadrant is the region represented by the inequations x ![]() 0 and y
0 and y ![]() 0.
0.
The feasible region determined by the system of constraints
2x + 5y ![]() 100, 40x + 25y
100, 40x + 25y![]() 1000, x
1000, x ![]() 0 and y
0 and y ![]() 0 are as follows
0 are as follows
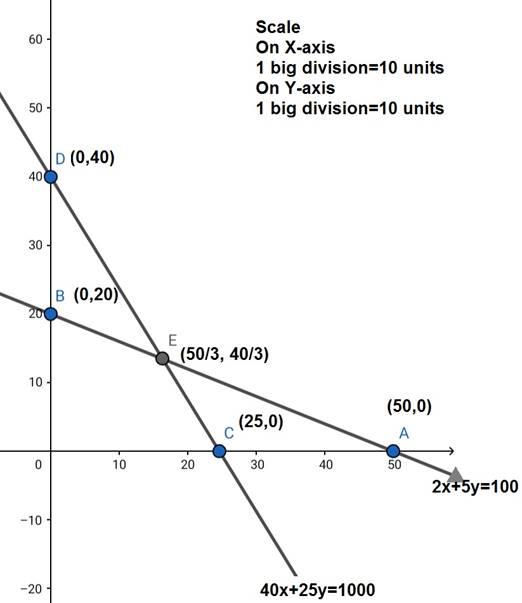
The corner points are O(0,0), B(0,20), E![]() , and C(25,0). The value of Z at these corner points are as follows:
, and C(25,0). The value of Z at these corner points are as follows:
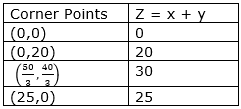
The maximum value of Z is 30 which is attained at E.
Thus, the maximum distance travelled by the young man is 30 kms, if he drives ![]() km at a speed of 25 km/hr and
km at a speed of 25 km/hr and ![]() km at a speed of 40 km/hr.
km at a speed of 40 km/hr.