Anil wants to invest at most ₹ 12000 in Saving Certificates and National Saving Bonds. According to rules, he has to invest at least ₹ 2000 in Saving Certificates and at least 4000 in National Saving Bonds. If the rate of interest on saving certificate is 8% per annum and the rate of interest on National Saving Bonds is 10% per annum, how much money should he invest to earn
maximum yearly income? Find also his maximum yearly income.
Let Anil invests Rs x and Rs y in saving certificate (SC) and National saving bond (NSB) respectively.
Since, the rate of interest on SC is 8% annual and on NSB is 10% annual. So, interest on Rs x of SC is ![]() and Rs y of NSB is
and Rs y of NSB is ![]() per annum.
per annum.
Let Z be total interest earned so,
Z = ![]() +
+ ![]()
Given he wants to invest Rs 12000 is total
x + y![]() 12000
12000
According to the rules he has to invest at least Rs 2000 in SC and at least Rs 4000 in NSB.
x![]() 2000
2000
y ![]() 4000
4000
Hence the mathematical formulation of LPP is to find x and y which
Maximizes Z
Max Z = ![]() +
+ ![]()
Subject to constraints
x![]() 2000
2000
y ![]() 4000
4000
x + y![]() 12000
12000
x,y ![]() 0
0
The region represented by x![]() 2000: line x = 2000 is parallel to the y - axis and passes through (2000,0).
2000: line x = 2000 is parallel to the y - axis and passes through (2000,0).
The region not containing the origin represents x![]() 2000
2000
As (0,0) doesn’t satisfy the inequation x![]() 2000
2000
The region represented by y ![]() 4000: line y = 4000 is parallel to the x - axis and passes through (0,4000).
4000: line y = 4000 is parallel to the x - axis and passes through (0,4000).
The region not containing the origin represents y![]() 4000
4000
As (0,0) doesn’t satisfy the inequation y![]() 4000
4000
Region represented by x + y![]() 12000: line x + y = 12000 meets axes at A(12000,0) and B(0,12000) respectively. The region which contains the origin represents the solution set of x + y
12000: line x + y = 12000 meets axes at A(12000,0) and B(0,12000) respectively. The region which contains the origin represents the solution set of x + y![]() 12000
12000
as (0,0) satisfies the inequality x + y![]() 12000.
12000.
Region x,y ![]() 0 is represented by the first quadrant.
0 is represented by the first quadrant.
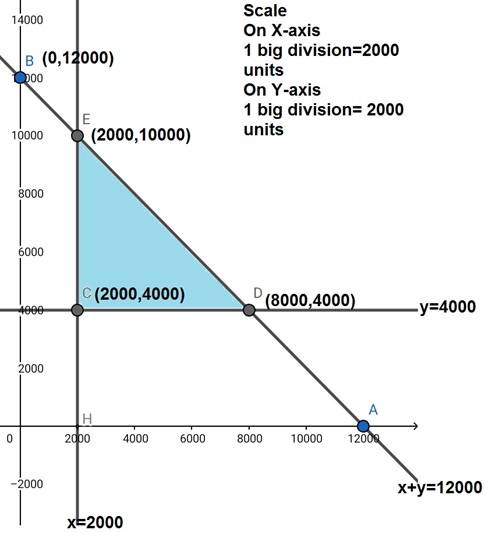
The corner points are E(2000,10000), C(2000,4000), D(8000,4000).
The values of Z at these corner points are as follows:
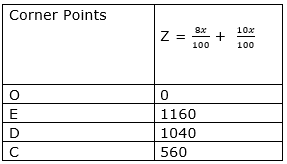
The maximum value of Z is Rs 1160 which is attained at E(2000,10000).
Thus the maximum earning is Rs1160 obtained when Rs 2000 were invested in SC and Rs 10000 in NSB.