A total amount of ₹7000 is deposited in three different saving bank accounts with annual interest rates of 5%, 8% and respectively. The total annual interest from these three accounts is ₹550. Equal amounts have been deposited in the 5% and 8% savings accounts. Find the amount deposited in each of the three accounts, with the help of matrices.

Let the deposited be x, y and z respectively.

As per the Data we get,

x + y + z = 7000

5%x + 8%y + 8.5%z = 550

i.e 5x + 8y + 8.5z = 55000

x – y = 0

These three equations can be written as

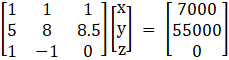
A X = B

|A| = 1(0 + 8.5) – 1(0 – 8.5) + 1(– 5 – 8)

= 1(8.5) – 1(– 8.5) + 1(– 13)

= 8.5 + 8.5 – 13

= 4

Hence, the unique solution given by x = A ^{– 1}B

C_{11 =} (– 1)^{1 + 1} (0 + 8.5) = 8.5

C₁₂ = (– 1)^{1 + 2} (0 – 8.5) = 8.5

C₁₃ = (– 1)^{1 + 3} (– 5 – 8) = – 13

C₂₁ = (– 1)^{2 + 1} (0 + 1) = – 1

C₂₂ = (– 1)^{2 + 2} (0 – 1) = – 1

C₂₃ = (– 1)^{2 + 3} (– 1 – 1 ) = 2

C₃₁ = (– 1)^{3 + 1} (8.5 – 8) = 0.5

C₃₂ = (– 1)^{3 + 2} (8.5 – 5) = – 3.5

C₃₃ = (– 1)^{3 + 3} (8 – 5) = 3

Adj A =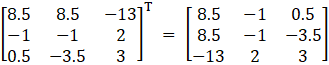

X = A ^{– 1} B =

X =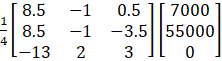

X =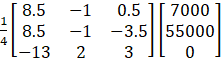

X =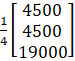

=

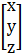Hence, x = 1125, y = 1125 and z = 4750