Verify Rolle’s theorem for each of the following functions on the indicated intervals :

Question

Philoid · Accepted Answer

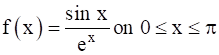
First, let us write the conditions for the applicability of Rolle’s theorem:

For a Real valued function ‘f’:

a) The function ‘f’ needs to be continuous in the closed interval [a,b].

b) The function ‘f’ needs differentiable on the open interval (a,b).

c) f(a) = f(b)

Then there exists at least one c in the open interval (a,b) such that f’(c) = 0.

Given function is:

⇒ on [0,]

This can be written as

⇒ f(x) = e ^{– x}sinx on [0,]

We know that exponential and sine functions are continuous and differentiable on R.

Let’s find the values of the function at an extremum,

⇒ f(0) = e ^{– 0}sin(0)

⇒ f(0) = 1×0

⇒ f(0) = 0

⇒

We got , so there exist a such that f’(c) = 0.

Let’s find the derivative of f(x)

⇒

⇒ f’(x) = sinx( – e ^{– x}) + e ^{– x}(cosx)

⇒ f’(x) = e ^{– x}( – sinx + cosx)

We have f’(c) = 0,

⇒ e ^{– c}( – sinc + cosc) = 0

⇒ – sinc + cosc = 0

⇒

∴ Rolle’s theorem is verified.