In a binomial distribution, the sum and product of the mean and the variance are 25/3 and 50/3 respectively. Find the distribution.
Let n and p be the parameters of the required binomial distribution. So,
1 - p = q
![]()
![]()
![]()
![]()
Also,
![]()
![]()
![]()
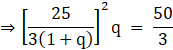
![]()
⇒625q = 150[(1+q)2]
⇒25q = 6[(1+q)2]
⇒6 + 6q2 + 12q – 25q = 0
⇒6q2 – 13q + 6 = 0
⇒6q2 – 9q - 4q + 6 = 0
⇒3q(2q - 3) - 2(2q - 3) = 0
⇒(2q - 3)(3q - 2) = 0
⇒(2q - 3) = 0 or (3q - 2) = 0
![]()
As, q≤1
![]()
Now, p = 1 - q
![]()
![]()
![]()
![]()
![]()
⇒n = 15
The required binomial distribution is given by,
![]()
6