Draw a circle of radius 4cm form a point on the concentric circle of radius 6cm and measure its length. Also, verify the measurement by actual calculation.

Step1: Draw a circle of radius 4 cm with centre O by taking 4 cm in compass. This is the inner circle

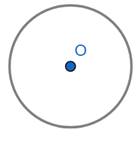
Step2: Now take 6 cm in compass keep the needle on point O and draw a circle. This is the outer circle. Take any point P on the outer circle

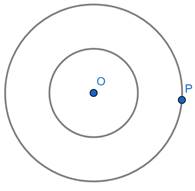
Now we have to draw a tangent from point P to the inner circle. This is the same as drawing tangents to circle from an external point.

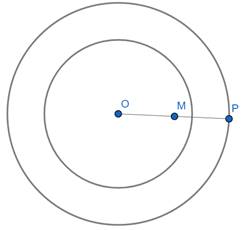
Step4: Join OP and using scale mark the midpoint of OP as M

Step5: Take the distance MO in compass keep the needle on point M and mark arcs cutting the inner circle at point Q and T as shown

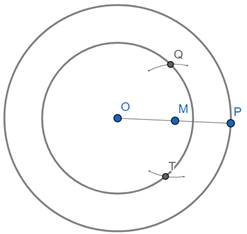
Step6: Construct a line passing through PQ and PT which are the required tangents and measure the lengths PQ and PT using a scale

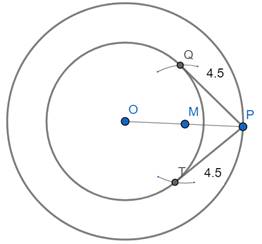
For verification

Let's join OQ

⇒ ∠OQP = 90° …radius OQ is perpendicular to tangent PQ at the point of contact Q

Consider ΔOQP

⇒ OQ = 4 cm …radius of inner circle

⇒ OP = 6 cm …radius of outer circle

Using Pythagoras

⇒ OP² = OQ² + PQ²

⇒ 6² = 4² + PQ²

⇒ 36 = 16 + PQ²

⇒ PQ² = 20

⇒ PQ = √20

⇒ PQ = √(5 × 4)

⇒ PQ = 2√5

⇒ PQ = 4.5 cm

Hence verified