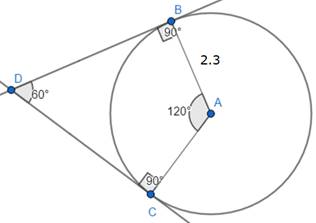
Draw a pair of tangents to a circle of radius 2.3 cm which is inclined to each other at an angle of 60°.

Question

Philoid · Accepted Answer

Consider a rough figure as shown DB and DC are tangents centre of circle is A

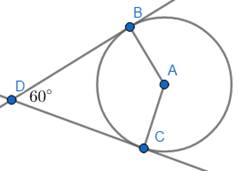
In quadrilateral ABDC

∠BDC = 60° …given

∠DBA = 90° …radius is perpendicular to tangent at point of contact

∠DCA = 90° …radius is perpendicular to tangent at point of contact

As the sum of angles of a quadrilateral is 360°

⇒ ∠BDC + ∠DBA + ∠DCA + ∠BAC = 360°

⇒ 60° + 90° + 90° + ∠BAC = 360°

⇒ 240° + ∠BAC = 360°

⇒ ∠BAC = 120°

Now let us construct

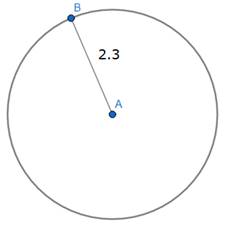
Step1: Construct a circle of radius 2.3 cm mark the centre as A and draw radius AB

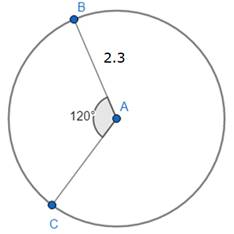
Step2: Using protractor draw the line at 120° to AB from point A and mark its intersection point with a circle as C join AC

Step3: Using protractor draw a line perpendicular to AB from point B because tangent is perpendicular to the radius. Thus this line is tangent to circle at point B

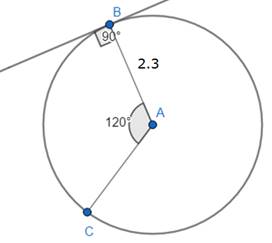
Step4: Using protractor draw a line perpendicular to AC from point C and mark the intersection point with a line drawn in step3 as D

Hence tangents DB and DC are ready at angle 60°