In a circle of radius 21 cm, and arc subtends an angle of 60° at the centre. Find

(i) length of arc

(ii) area of the sector formed by the arc

(iii) area of the segment formed by the corresponding chord of the arc.

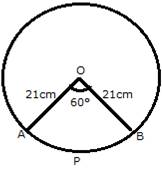
Given: Radius of the circle = OA =OB = 21cm

and θ = 60°

(i) Length of the arc

= 22cm

(ii) Area of the sector formed by this arc

= 11 × 21

= 231 cm²

(iii) area of the segment formed by the corresponding chord of the arc

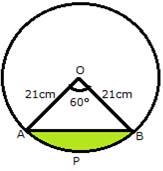
In ΔOAB,

∠OAB = ∠OBA (As OA = OB)

∠OAB + ∠AOB + ∠OBA = 180°

2∠OAB + 60° = 180°

∠OAB = 60°

∴ ΔOAB is an equilateral triangle.

Area of segment APB = Area of sector OAPB − Area of ΔOAB