Examine, seeing the graph of the polynomials given below, whether they are a linear or quadratic polynomial or neither linear nor quadratic polynomial:
(i)  (ii)
(ii) 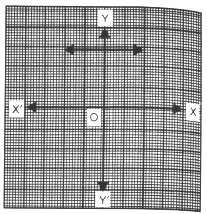
(iii)  (iv)
(iv) 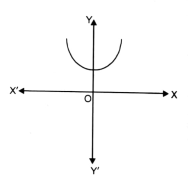
(v)  (vi)
(vi) 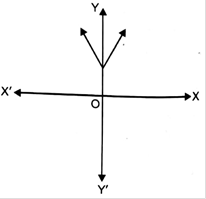
(vii)  (viii)
(viii) 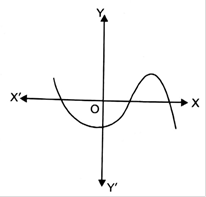
(i) In general, we know that for a linear polynomial ax + b, a≠0, the graph of y = ax + b is a straight line which intersects the x – axis at exactly one point.
And here, we can see that the graph of y = p(x) is a straight line and intersects the x – axis at exactly one point. Therefore, the given graph is of a Linear Polynomial.
(ii) Here, the graph of y = p(x) is a straight line and parallel to the x – axis . Therefore, the given graph is of a Linear Polynomial.
(iii) For any quadratic polynomial ax2 + bx + c, a ≠ 0, the graph of the corresponding equation y = a x2 + bx + c has one of the two shapes either open upwards like ![]() or open downwards like
or open downwards like ![]() depending on whether a > 0 or a < 0. (These curves are called parabolas.)
depending on whether a > 0 or a < 0. (These curves are called parabolas.)
Here, we can see that the shape of the graph is a parabola. Therefore, the given graph is of a Quadratic Polynomial.
(iv) For any quadratic polynomial ax2 + bx + c, a ≠ 0, the graph of the corresponding equation y = ax2 + bx + c has one of the two shapes either open upwards like ![]() or open downwards like
or open downwards like ![]() depending on whether a > 0
depending on whether a > 0![]() or a < 0. (These curves are called parabolas.)
or a < 0. (These curves are called parabolas.)
Here, we can see that the shape of the graph is parabola. Therefore, the given graph is of a Quadratic Polynomial.
(v) The shape of the graph is neither a straight line nor a parabola. So, the graph is not of a linear polynomial nor a quadratic polynomial.
(vi) The given graph have a straight line but it doesn’t intersect at x – axis and the shape of the graph is also not a parabola. So, it is not a graph of a quadratic polynomial. Therefore, it is not a graph of linear polynomial or quadratic polynomial.
(vii) The shape of the graph is neither a straight line nor a parabola. So, the graph is not of a linear polynomial or a quadratic polynomial.
(viii) The shape of the graph is neither a straight line nor a parabola. So, the graph is not of a linear polynomial or a quadratic polynomial.