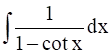Evaluate the integral

Ideas required to solve the problems:

* Integration by substitution: A change in the variable of integration often reduces an integral to one of the fundamental integration. If derivative of a function is present in an integration or if chances of its presence after few modification is possible then we apply integration by substitution method.

* Knowledge of integration of fundamental functions like sin, cos ,polynomial, log etc and formula for some special functions.

Let, I =

To solve such integrals involving trigonometric terms in numerator and denominators. We use the basic substitution method and to apply this simply we follow the undermentioned procedure-

If I has the form

Then substitute numerator as -

Where A, B and C are constants

We have, I =

As I matches with the form described above, So we will take the steps as described.

∴

⇒ {

⇒

Comparing both sides we have:

C = 0

A – B = 0 ⇒ A = B

B + A = 1 ⇒ 2A = 1 ⇒ A = 1/2

∴ A = B = 1/2

Thus I can be expressed as:

I =

I =

∴ Let I₁ = and I₂ =

⇒ I = I₁ + I₂ ….equation 1

I₁ =

Let, u = sin x – cos x ⇒ du = (cos x + sin x)dx

So, I₁ reduces to:

I₁ =

∴ I₁ = …..equation 2

As, I₂ =

∴ I₂ = …..equation 3

From equation 1 ,2 and 3 we have:

I =

∴ I =