Evaluate the following integrals –
![]()
Let ![]()
Let us assume ![]()
![]()
We know ![]() and derivative of a constant is 0.
and derivative of a constant is 0.
⇒ x + 1 = λ(2x2-1 + 1 + 0) + μ
⇒ x + 1 = λ(2x + 1) + μ
⇒ x + 1 = 2λx + λ + μ
Comparing the coefficient of x on both sides, we get
2λ = 1 ⇒ ![]()
Comparing the constant on both sides, we get
λ + μ = 1
![]()
![]()
Hence, we have ![]()
Substituting this value in I, we can write the integral as
![]()
![]()
![]()
![]()
Let ![]()
Now, put x2 + x + 1 = t
⇒ (2x + 1)dx = dt (Differentiating both sides)
Substituting this value in I1, we can write
![]()
![]()
Recall ![]()

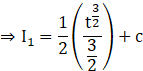
![]()
![]()
![]()
Let ![]()
We can write ![]()
![]()
![]()
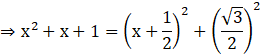
Hence, we can write I2 as
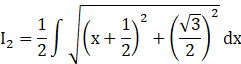
Recall ![]()
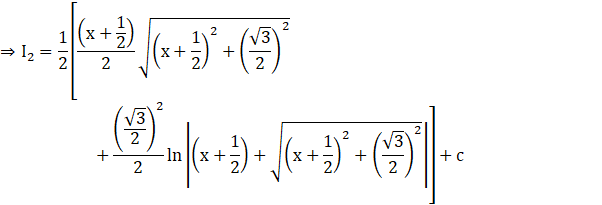
![]()
![]()
Substituting I1 and I2 in I, we get
![]()
Thus, 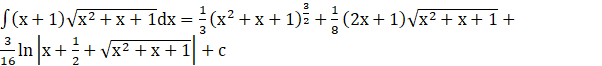
7