Evaluate the following integral:

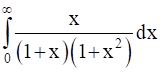
Let us assume

Adding – 1 and + 1

–

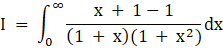
Let

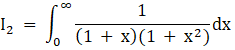
Thus I = I₁ – I₂ …….equation 1

Solving for I₁

since

I₁ = [tan ^{– 1}(∞) – tan ^{– 1}(0)]

I₁ = π/2 ……….equation 2

Solving for I₂

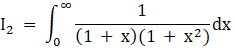
Let .....…..equation 3

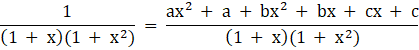
a + b = 0; a + c = 1; b + c = 0

solving we get

a = c = 1/2

b = – 1/2

substituting the values in equation 3

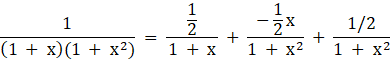
Thus substituting the values in I₂, thus

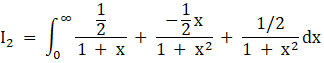
Solving :

Let 1 + x² = y

2xdx = dy

For x = ∞

y = ∞

For x = 0

y = 0

substituting values

Thus

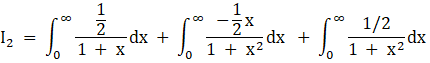
……….equation 4

Substituting values equation 2 and equation 4 in equation 1

Thus

I = I_{1 –} I₂

I = π/2 – π/4

I = π/4