Evaluate the following integral:
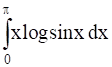
Let us assume![]() ….....equation 1
….....equation 1
By property, we know that ![]()
![]() .....………equation 2
.....………equation 2
Adding equation 1 and equation 2

We know
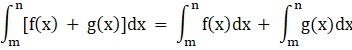
![]() ……….equation 3
……….equation 3
We know ![]()
![]() if f(2a – x) = f(x)
if f(2a – x) = f(x)
= 0 if f(2a – x) = – f(x)
Thus equation 3 becomes
![]() ………equation 4 since logsin(π – x) = logsinx
………equation 4 since logsin(π – x) = logsinx
By property, we know that ![]()

![]() ………equation 5
………equation 5
Adding equation 4 and equation 5
![]() +
+ ![]()
We know
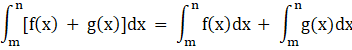
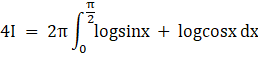
We know logm + logn = logmn thus
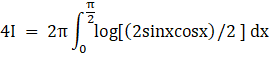

![]() since log(m/n) = logm – logn
since log(m/n) = logm – logn
![]() .....equation 6
.....equation 6
Let ![]()
Let 2x = y
2dx = dy
dx = dy/2
For x = 0
y = 0
for ![]()
y = π
thus substituting value in I1

From equation 3 we get
![]()
![]()
Thus substituting the value of I1 in equation 6
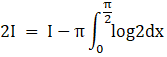
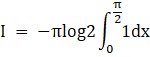
![]()
![]()
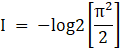
14