Solve the following differential equations:

Question

Philoid · Accepted Answer

Given

This is a first order linear differential equation of the form

Here, P = y^–2 and Q = y^–3

The integrating factor (I.F) of this differential equation is,

We have

Hence, the solution of the differential equation is,

Let

[Differentiating both sides]

By substituting this in the above integral, we get

Recall

⇒ xt = –{t log t – t} + c

⇒ xt = –t log t + t + c

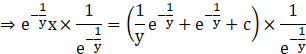
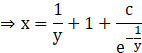
Thus, the solution of the given differential equation is