Solve the following differential equations:

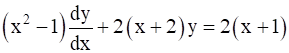
Given

[∵ x² – 1 = (x + 1)(x – 1)]

This is a first order linear differential equation of the form

Here, and

The integrating factor (I.F) of this differential equation is,

We have and

[∵ m log a = log a^m]

[∵ log a + log b = log ab]

[∵ e^{log x} = x]

Hence, the solution of the differential equation is,

We can write (x – 1)² = (x + 1)² – 4x

Recall and

Thus, the solution of the given differential equation is