Solve each of the following initial value problems:

, y(0) = 0

, y(0) = 0

Given and y(0) = 0

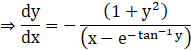
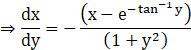
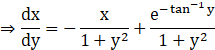
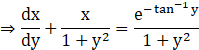
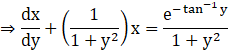
This is a first order linear differential equation of the form

Here, and

The integrating factor (I.F) of this differential equation is,

We have

Hence, the solution of the differential equation is,

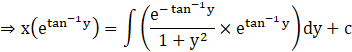
We know

However, when x = 0, we have y = 0

⇒ 0 = (0 + c)e⁰

⇒ 0 = (c) × 1

∴ c = 0

By substituting the value of c in the equation for x, we get

Thus, the solution of the given initial value problem is