A, B and C in order toss a coin. The one to throw a head wins. What are their respective chances of winning assuming that the game may continue indefinitely?

Question

Philoid · Accepted Answer

Given that A, B and C toss a coin until one of them gets a head to win the game.

Let us find the probability of getting the head.

⇒ P(A_H) = P(A getting a head on tossing a coin)

⇒

⇒ P(A_N) = P(A not getting head on tossing a coin)

⇒

⇒ P(B_H) = P(B getting a head on tossing a coin)

⇒

⇒ P(B_N) = P(B not getting head on tossing a coin)

⇒

⇒ P(C_H) = P(C getting a head on tossing a coin)

⇒

⇒ P(C_N) = P(C not getting head on tossing a coin)

⇒

It is told that A starts the game.

A tosses in1^st,4^th,7^th,…… tosses.

This can be shown as follows:

⇒ P(W_A) = P(A wins the game)

⇒ P(W_A) = P(A_H) + P(A_NB_NC_NA_H) + P(A_NB_NC_NA_NB_NC_NA_H) + …………………

Since tossing a coin by each person is an independent event, the probabilities multiply each other.

⇒ P(W_A) = (P(A_H)) + (P(A_N)P(B_N)P(C_N)P(A_H)) + ………………

⇒

The terms in the bracket resembles the infinite geometric series sequence:

We know that the sum of a Infinite geometric series with first term ‘a’ and common ratio ‘r’ is

⇒

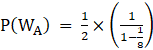
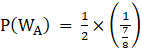
B tosses in2^nd,5^th,8^th,…… tosses.

This can be shown as follows:

⇒ P(W_B) = P(B wins the game)

⇒ P(W_B) = P(A_NB_H) + P(A_NB_NC_NA_NB_H) + P(A_NB_NC_NA_NB_NC_NA_NB_H) + …………………

Since tossing a coin by each person is an independent event, the probabilities multiply each other.

⇒ P(W_B) = (P(A_N)P(B_H)) + (P(A_N)P(B_N)P(C_N)P(A_N)P(B_H)) + ………………

⇒

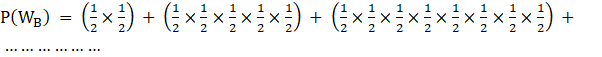
The terms in the bracket resembles the infinite geometric series sequence:

We know that the sum of a Infinite geometric series with first term ‘a’ and common ratio ‘r’ is

⇒

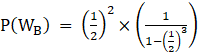
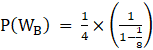
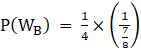
⇒ P(W_C) = P(winning of C)

⇒ P(W_C) = 1-P(W_A)-P(W_B)

⇒

∴ The chances of winning of A,B and C are .