It is known that 60% of mice inoculated with serum are protected from a certain disease. If 5 mice are inoculated, find the probability that

i. none contract the disease

ii. more than 3 contract the disease.

Given that, the probability that the mice are protected from a certain disease is 60%.

Also, the sample size of mice = 5

Let p be the probability of the mice not contracting with a certain disease.

Then, q is the probability of the mice contracting with a certain disease.

⇒ p = 60%

And we know that,

p + q = 1

⇒ q = 1 – p

Let X be a random variable representing a number of mice contracting with the disease.

Then, the probability of r mice contracting with the disease out of n mice inoculated is given by the following binomial distribution.

P (X = r) = ⁿC_rq^rp^n-r

Putting the values,

n = 5,

&

We get

…(A)

(i). We need to find the probability that none of the mice contract with the disease.

For this, put r = 0.

We get the probability as,

Probability = P (X = 0)

From equation (A),

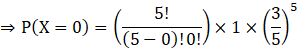
⇒ P (X = 0) = 0.07776

∴, the probability that none of the mice contracts with the disease is 0.07776.

(ii). We need to find the probability that more than 3 mice contract the disease.

So, probability = P (X = 4) + P (X = 5)

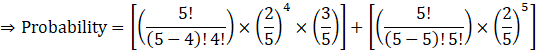
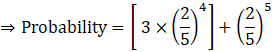
⇒ Probability = 0.2125

∴, the probability that more than 3 mice contract the disease is 0.2125.