From a lot of 30 bulbs which include 6 defectives, a sample of 4 bulbs is drawn at random with replacement. Find the probability distribution of the number of defective bulbs.

Given that, there are 30 bulbs, which include 6 defective bulbs.

A sample of 4 bulbs is drawn at random with replacement.

Let p be the probability of defective bulbs.

Since 6 bulbs are defective out of 30 bulbs.

Then, let q be the probability of fine bulbs.

And we know, p + q = 1

⇒ q = 1 – p

Let X denote a random variable representing a number of defective bulbs out of 4 bulbs drawn at random.

So, Binomial distribution of getting r successes out of 4 bulbs drawn at random is given by

P (X = r) = ⁿC_rp^rq^n-r

Here, n = 4.

Now, substituting values of n, p and q in the formula P (X = r). We get

…(i)

We need to find the probability distribution of the number of successes.

The probability of 0 defective bulb in 4 sample bulbs is given by,

Probability = P (X = 0)

Put r = 0 in (i),

The probability of 1 defective bulb in 4 sample bulbs is given by,

Probability = P (X = 1)

Put r = 1 in (i),

The probability of 2 successes in 4 throws is given by,

Probability = P (X = 2)

Put r = 2 in (i),

The probability of 3 successes in 4 throws is given by,

Probability = P (X = 3)

Put r = 3 in (i),

The probability of 4 successes in 4 throws is given by,

Probability = P (X = 4)

Put r = 4 in (i),

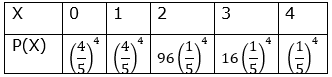
Thus, the probability distribution is