If f(x) be defined on [–2, 2] and is given by  and g(x) = f(|x|) + |f(x)|. Find g(x).
and g(x) = f(|x|) + |f(x)|. Find g(x).
Given ![]() and g(x) = f(|x|) + |f(x)|
and g(x) = f(|x|) + |f(x)|
Now, we have ![]()
However, |x| ≥ 0 ⇒ f(|x|) = |x| – 1 when 0 ≤ |x| ≤ 2
We also have ![]()
![]()
We know ![]()
![]()
Here, we are interested only in the range [0, 2].
![]()
Substituting this value of |x – 1| in |f(x)|, we get
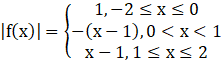
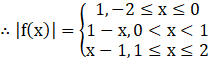
We need to find g(x).
g(x) = f(|x|) + |f(x)|
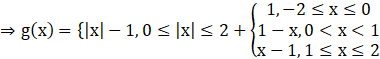
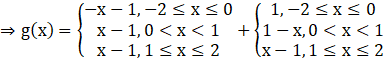
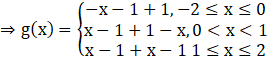
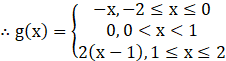
Thus, 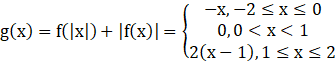
3