Let f, g be two real functions defined by and . Then, describe each of the following functions.

i. f + g

ii. g – f

iii. fg

iv.

v.

vi.

vii. f² + 7f

viii.

Given and

We know the square of a real number is never negative.

Clearly, f(x) takes real values only when x + 1 ≥ 0

⇒ x ≥ –1

∴ x ∈ [–1, ∞)

Thus, domain of f = [–1, ∞)

Similarly, g(x) takes real values only when 9 – x² ≥ 0

⇒ 9 ≥ x²

⇒ x² ≤ 9

⇒ x² – 9 ≤ 0

⇒ x² – 3² ≤ 0

⇒ (x + 3)(x – 3) ≤ 0

⇒ x ≥ –3 and x ≤ 3

∴ x ∈ [–3, 3]

Thus, domain of g = [–3, 3]

i. f + g

We know (f + g)(x) = f(x) + g(x)

Domain of f + g = Domain of f ∩ Domain of g

⇒ Domain of f + g = [–1, ∞) ∩ [–3, 3]

∴ Domain of f + g = [–1, 3]

Thus, f + g : [–1, 3] → R is given by

ii. f – g

We know (f – g)(x) = f(x) – g(x)

Domain of f – g = Domain of f ∩ Domain of g

⇒ Domain of f – g = [–1, ∞) ∩ [–3, 3]

∴ Domain of f – g = [–1, 3]

Thus, f – g : [–1, 3] → R is given by

iii. fg

We know (fg)(x) = f(x)g(x)

As earlier, domain of fg = [–1, 3]

Thus, f – g : [–1, 3] → R is given by

iv.

We know

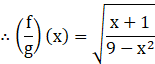
As earlier, domain of = [–1, 3]

However, is defined for all real values of x ∈ [–1, 3], except for the case when 9 – x² = 0 or x = ±3

When x = ±3, will be undefined as the division result will be indeterminate.

⇒ Domain of = [–1, 3] – {–3, 3}

∴ Domain of = [–1, 3)

Thus, : [–1, 3) → R is given by

v.

We know

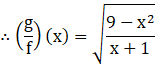
As earlier, domain of = [–1, 3]

However, is defined for all real values of x ∈ [–1, 3], except for the case when x + 1 = 0 or x = –1

When x = –1, will be undefined as the division result will be indeterminate.

⇒ Domain of = [–1, 3] – {–1}

∴ Domain of = (–1, 3]

Thus, : (–1, 3] → R is given by

vi.

We know (f – g)(x) = f(x) – g(x) and (cf)(x) = cf(x)

As earlier, Domain of = [–1, 3]

Thus, : [–1, 3] → R is given by

vii. f² + 7f

We know (f² + 7f)(x) = f²(x) + (7f)(x)

⇒ (f² + 7f)(x) = f(x)f(x) + 7f(x)

Domain of f² + 7f is same as domain of f.

∴ Domain of f² + 7f = [–1, ∞)

Thus, f² + 7f : [–1, ∞) → R is given by

viii.

We know and (cg)(x) = cg(x)

Domain of = Domain of g = [–3, 3]

However, is defined for all real values of x ∈ [–3, 3], except for the case when 9 – x² = 0 or x = ±3

When x = ±3, will be undefined as the division result will be indeterminate.

⇒ Domain of = [–3, 3] – {–3, 3}

∴ Domain of = (–3, 3)

Thus, : (–3, 3) → R is given by