A student has to answer 10 questions, choosing at least 4 from each of part A and part B. If there are 6 questions in part A and 7 in part B, in how many ways can the student choose 10 questions?

Given that 10 questions are to be answered by part A and part B by choosing at least 4 from each part.

It is also mentioned that there are 6 questions in part A and 7 in part B.

There are 3 cases to answer 10 questions:

i. 4 from part A and 6 from part B

ii. 5 from part A and 5 from part B

iii. 6 from part A and 4 from part B

Let us assume the total no. of ways of answering 10 questions be N.

⇒ N = no. of ways of answering 10 questions from both parts

⇒ N = (No. of ways of answering 4 questions from part A and 6 from part B) + (No. of ways of answering 5 questions from part A and 5 questions from part B) + (No. of ways of answering 6 questions from part A and 4 from part B)

⇒ N = (⁶C₄ × ⁷C₆) + (⁶C₅ × ⁷C₅) + (⁶C₆ × ⁷C₄)

We know that ,

And also n! = (n)(n – 1)......2.1

⇒

⇒

⇒

⇒

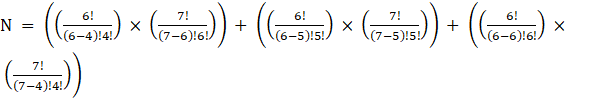
⇒ N = 105 + 126 + 35

⇒ N = 266

∴ The total no. of ways of answering 10 questions is 266 ways.